Nội dung chính
Thuật toán Naive Bayes
Bayesian là một giải thuật dựa trên phép toán xác xuất. Chúng có thể dự đoán tỷ lệ thuộc lớp nào đó, giống như tỷ lệ mà cái mà mẫu thuộc về trong lớp. Giải thuật Bayesian dựa trên lý thuyết Bayes. Naive Bayes dược xem như là ảnh hưởng của giá trị thuộc tính trên lớp đưa vào là không phụ thuộc và các giá trị thuộc tính khác. Giả định này được gị là lớp điều kiện không phụ thuộc. Nó được làm đơn giản hóa vào tính toán và được gọi như là “naive” – ngây thơ.1.1 Định lý Bayes
Hãy coi X ={x1, x2,…,xn} là một mẫu, các thành phần này biểu diễn giá trị trên tập n thuộc tính. Trong định lý Bayes, X được xem xét là một minh chứng. Hãy H là một vài giả thuyết, như là dữ liệu X thuộc vào một lớp đặc biệt C. Cho các vấn đề phân lớp, mục tiêu của chúng ta là quyết đinh P(H|X) cái mà là xác xuất cái mà giả thuyết H năm được các chứng cứ. Nói một cách khác, chúng ta tìm xác xuyết cái mà mẫu X thuộc vào lớp C, cái mà được đưa ra cho chúng ta biết về mô tả thuộc tính của X. P(H|X) chính là xác xuất của H mà điều kiện là X. Dựa trên định lý Bayes, xác xuất cái mà chúng ta muốn tình P(H|X) có thể được biểu diễn gồm các xác xuất sau: P(X|H) và P(X) và dduwowcj tính như sau : P(H|X) = P(X|H).P(H)/P(X)
1.2 Giải thuật phân lớp Naive bayes
Giải thuật phân lớp Bayes được làm việc theo luồng sau:
a. Hãy cho tập mẫu training là T, mỗi lớp sẽ có một label, chúng ta có k lớp. Mỗi mẫu sẽ được biểu diễn bởi một vector n chiều, X={x1,x2,…,xn}, dự đoán n tính các giá trị của n thuộc tính, A1, A2, ….An tương ứng.
b. Giả sử có m lớp C1, C2,..,Cm. Cho một phần tử dữ liệu X, bộ phân lớp sẽ gán nhãn cho X là lớp có xác suất hậu nghiệm lớn nhất. Cụ thể, bộ phân lớp Bayes sẽ dự đoán X thuộc vào lớp Ci nếu và chỉ nếu:
P(Ci|X) > P(Cj|X) (1<= i, j <=m, i != j)
Giá trị này sẽ tính dựa trên định lý Bayes.
c.Để tìm xác suất lớn nhất, ta nhận thấy các giá trị P(X) là giống nhau với mọi lớp nên không cần tính. Do đó ta chỉ cần tìm giá trị lớn nhất của P(X|Ci) * P(Ci). Chú ý rằng P(Ci) được ước lượng bằng |Di|/|D|, trong đó Di là tập các phần tử dữ liệu thuộc lớp Ci. Nếu xác suất tiền nghiệm P(Ci) cũng không xác định được thì ta coi chúng bằng nhau P(C1) = P(C2) = … = P(Cm), khi đó ta chỉ cần tìm giá trị P(X|Ci) lớn nhất.
d. Khi số lượng các thuộc tính mô tả dữ liệu là lớn thì chi phí tính toàn P(X|Ci) là rất lớn, dó đó có thể giảm độ phức tạp của thuật toán Naive Bayes giả thiết các thuộc tính độc lập nhau. Khi đó ta có thể tính:
P(X|Ci) = P(x1|Ci)…P(xn|Ci)
Làm mịn Laplace
Làm mịn Laplace là một kỹ thuật làm mịn giúp giải quyết vấn đề xác suất bằng không trong thuật toán học máy Naïve Bayes. Sử dụng các giá trị alpha cao hơn sẽ đẩy khả năng hướng tới giá trị 0,5, tức là xác suất của một từ bằng 0,5 cho cả đánh giá tích cực và tiêu cực. Vì chúng ta không nhận được nhiều thông tin từ đó, nên không thích hợp. Do đó, chúng ta ưu tiên sử dụng alpha = 1.Xây dựng thuật toán Phân lớp Naive Bayes bằng C#
3. Một ví dụ của việc sử dụng giải thuật phân lớp Naive Bayes
Chúng ta có tập dữ liệu học tập sau đây:| TT | Tuổi | Thu nhập | Sinh viên | Tín dụng | Ci: Mua |
| 1 | Trẻ | Cao | Không | Cao | không |
| 2 | Trẻ | Cao | Không | rất cao | không |
| 3 | Trung niên | Cao | Không | cao | Có |
| 4 | Cao niên | Trung bình | Không | cao | Có |
| 5 | Cao niên | Thấp | Có | cao | Có |
| 6 | Trung niên | Thấp | Có | Rất cao | không |
| 7 | Trẻ | Thấp | Có | Rất cao | Có |
| 8 | Trẻ | Trung bình | Không | Cao | không |
| 9 | Trẻ | Thấp | Có | Cao | Có |
| 10 | Cao niên | Trung bình | Có | Cao | Có |
| 11 | Trẻ | Trung bình | Có | Rất cao | Có |
| 12 | Trung niên | Trung bình | Không | Rất cao | Có |
| 13 | Trung niên | Cao | Có | Cao | Có |
| 14 | Cao niên | Trung bình | Không | Rất cao | Không |
Dữ liệu trên được mô tả bởi các thuộc tính: tuổi, thu nhập, là sinh viên hay không và tài khoản tín dụng. Có 2 thuộc tính được gán nhãn cho việc người đó có mua máy tính hay không đó là có (class C1), không (class C2)
Giả sử mẫu dữ liệu mà chúng ta cần dự đoán là:
X = (tuổi = trẻ, thu nhập=trung bình, sinh viên = có, tài khoản tín dụng = cao)
Chúng ta cần tối ưu phép toán P(X|Ci) P(Ci) cho i = 1,2. P(Ci), là xác xuất của mỗi lớp. có thể được dự đoán dựa trên các mẫu đã học:
P(mua=có) = 9/14
P(mua=không) = 5/14
Để tính toán P(X|Ci), cho i =1,2, chngs ta tính toán tỉ lệ xác xuất có điều kiện như sau:
P(tuổi=trẻ|mua=có) = 2/9
P(tuổi=trẻ|mua=không) =3/5
P=(thu nhập=trung bình|mua=có)=4/9
P(thu nhâp=trung bình|mua=không) =2/5
P(sinh viên=có|mua=có) =6/9
P(sinh viên-có|mua=không)=1/5
…
Sử dụng các công thức tính xác xuất, chúng ta có:
P(X|mua=có) = 2/9×4/9×6/9×6/9 =0.044
Tương tự:
P(X|mua=0)=0.019
Để tìm lớp cái mà tối ưu P(X|Ci)P(Ci), Chúng ta có thể tính toán:
P(X|mua=có)xP(mua=có) = 0.028
P(X|mua=không)xP(mua=không) = 0.007
Vì vậy, giải thuật phân lớp Naive Bayes ở đây có thể dự đoán mua = có cho mẫu dữ liệu X.
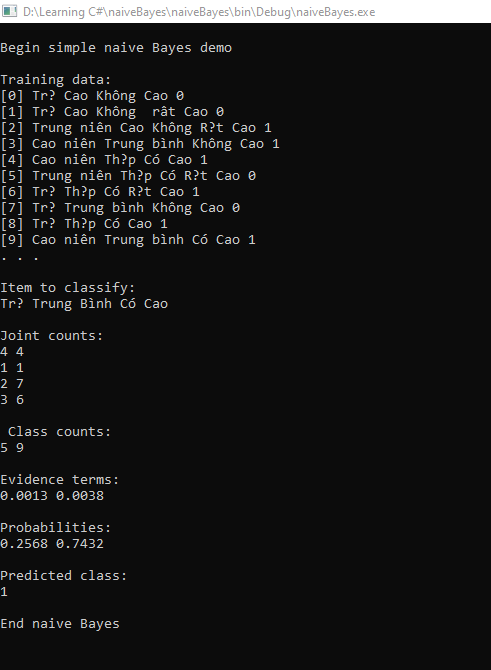
Xây dựng thuật toán naive bayes bằng C#, dưới đây là đoạn mã code thực hiện demo thuật toán Naive bayes sử dụng C#
Chúng ta có bài toán cần phân lớp:
// Load dữ liệu đàu vào
string fn = "D:/Learning C#/data2.txt";
int nx = 4; // Số thuộc tính một mẫu dữ liệu
int nc = 2; // Số Lớp
int N = 14; // Số mẫu data trong dữ liệu học tập
string[][] data = LoadData(fn, N, nx + 1, ',');
// Đọc data training
for (int i = 0; i < 10; ++i)
{
Console.Write("[" + i + "] ");
for (int j = 0; j < nx + 1; ++j)
{
Console.Write(data[i][j] + " ");
}
Console.WriteLine("");
}
//Dữ liệu cần dự đoán
int[][] jointCts = MatrixInt(nx, nc);
int[] yCts = new int[nc];
string[] X = new string[] { "Trẻ", "Trung Bình", "Có","Cao" };
Console.WriteLine("Item to classify: ");
for (int i = 0; i < nx; ++i)
Console.Write(X[i] + " ");
Console.WriteLine("\n");
for (int i = 0; i < N; ++i)
{
int y = int.Parse(data[i][nx]);
++yCts[y];
for (int j = 0; j < nx; ++j)
{
if (data[i][j] == X[j])
++jointCts[j][y];
}
}
// Laplacian smoothing
for (int i = 0; i < nx; ++i)
for (int j = 0; j < nc; ++j)
++jointCts[i][j];
Console.WriteLine("Joint counts: ");
for (int i = 0; i < nx; ++i)
{
for (int j = 0; j < nc; ++j)
{
Console.Write(jointCts[i][j] + " ");
}
Console.WriteLine("");
}
Console.WriteLine("\n Class counts: ");
for (int k = 0; k < nc; ++k)
Console.Write(yCts[k] + " ");
Console.WriteLine("\n");
// Compute evidence terms
double[] eTerms = new double[nc];
for (int k = 0; k < nc; ++k)
{
double v = 1.0;
for (int j = 0; j < nx; ++j)
{
v *= (double)(jointCts[j][k]) / (yCts[k] + nx);
}
v *= (double)(yCts[k]) / N;
eTerms[k] = v;
}
Console.WriteLine("Evidence terms:");
for (int k = 0; k < nc; ++k)
Console.Write(eTerms[k].ToString("F4") + " ");
Console.WriteLine("\n");
double evidence = 0.0;
for (int k = 0; k < nc; ++k)
evidence += eTerms[k];
double[] probs = new double[nc];
for (int k = 0; k < nc; ++k)
probs[k] = eTerms[k] / evidence;
Console.WriteLine("Probabilities: ");
for (int k = 0; k < nc; ++k)
Console.Write(probs[k].ToString("F4") + " ");
Console.WriteLine("\n");
int pc = ArgMax(probs);
Console.WriteLine("Predicted class: ");
Console.WriteLine(pc);
Console.WriteLine("\nEnd naive Bayes ");
Console.ReadLine();
static string[][] MatrixString(int rows, int cols)
{
string[][] result = new string[rows][];
for (int i = 0; i < rows; ++i)
result[i] = new string[cols];
return result;
}
static int[][] MatrixInt(int rows, int cols)
{
int[][] result = new int[rows][];
for (int i = 0; i < rows; ++i)
result[i] = new int[cols];
return result;
}
static string[][] LoadData(string fn, int rows,
int cols, char delimit)
{
string[][] result = MatrixString(rows, cols);
FileStream ifs = new FileStream(fn, FileMode.Open);
StreamReader sr = new StreamReader(ifs);
string[] tokens = null;
string line = null;
int i = 0;
while ((line = sr.ReadLine()) != null)
{
tokens = line.Split(delimit);
for (int j = 0; j < cols; ++j)
result[i][j] = tokens[j];
++i;
}
sr.Close(); ifs.Close();
return result;
}
static int ArgMax(double[] vector)
{
int result = 0;
double maxV = vector[0];
for (int i = 0; i < vector.Length; ++i)
{
if (vector[i] > maxV)
{
maxV = vector[i];
result = i;
}
}
return result;
}
Kết quả khi chạy chương trình: