làm sao để bạn biết những cây hải đường này có tầm quan trọng như nhau?

– Hercule Poirot –

Thuật toán học máy Logistic Regression

Hồi quy tuyến tín là một công cụ quan trọng trong khoa học xã hội và tự nhiên. Trong học máy, hồi quy tuyến tính là một giải thuật thọc máy giám sát cho bài toán phân lớp và nó rất gần với mạng lưới thần kinh (neural netowrks). Logistic regression có thể được sử dụng để phân loại 2 lớp hoặc nhiều lớp. Bài toán phân loại 2 lớp có thể đơn giản hơn và được xây dựng với hàm sigmoid và với bài toán phân loại nhiều lớp sẽ phức tạp hơn sử dụng hàm softmax function sẽ được trình bày trong bài viết này.

Sự khác nhau của giải thuật Logistic Regression và Naive Bayes

Như chúng ta đã biết, thuật toán phân lớp học máy có thể được phân loại thành 2 dạng giải thuật là giải thuật generativ và discriminative.

Điều khác nhau cơ bản của Giải thuật Naive Bayes và Logistic Regression là giải thuật hồi quy tuyến tính (Logistic regression) là dạng Discriminative và Naive Bayes là dạng Generative

Hồi quy tuyến tính nhị phân và hồi quy tuyến tính đa thức

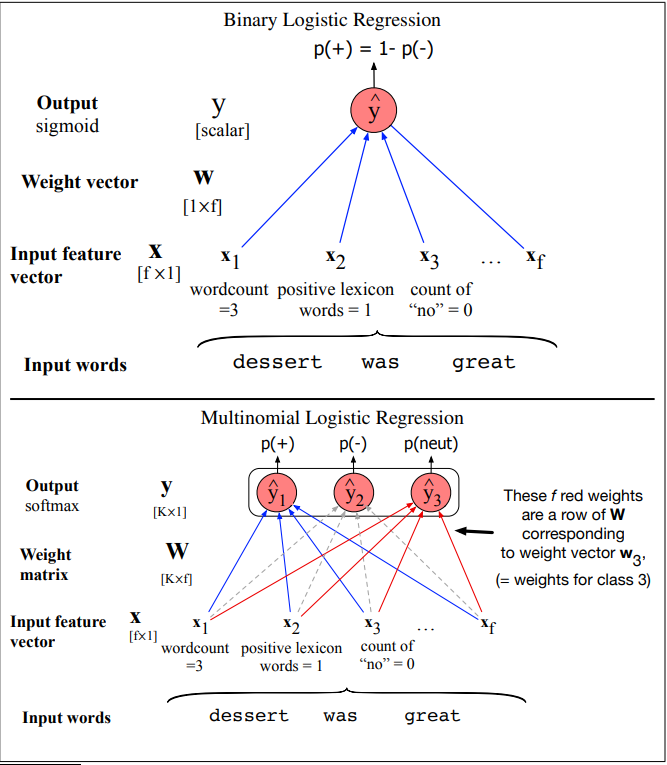
Hàm Sigmoid

Trong bài toán học máy phân lớp, hàm sigmoid được sử dụng khi dự liệu đầu vào để phân loại 2 lớp, hàm softmax được sử dụng khi dữ liệu đầu vào cần phân lớp là nhiều lớp.

Hàm Softmax

Dưới đây là hàm softmax được xây dựng bằng ngôn ngữ C# trong giải thuật logistic Regression

Hàm mất mát (Loss Function)

Tối ưu hàm mất mát

Demo Xây dựng Logistic Regression sử dụng ngôn ngữ C #

Tạo dữ liệu demo chương trình

 
            // dummy data
            // Make dummy Data 
            double[][] trainX = new double[27][];

            trainX[0] = new double[] { 0.1, 0.1 };  // lower left
            trainX[1] = new double[] { 0.1, 0.2 };
            trainX[2] = new double[] { 0.1, 0.3 };
            trainX[3] = new double[] { 0.2, 0.1 };
            trainX[4] = new double[] { 0.2, 0.2 };
            trainX[5] = new double[] { 0.2, 0.3 };
            trainX[6] = new double[] { 0.3, 0.1 };
            trainX[7] = new double[] { 0.3, 0.2 };
            trainX[8] = new double[] { 0.3, 0.3 };

            trainX[9] = new double[] { 0.4, 0.1 };  // lower right
            trainX[10] = new double[] { 0.4, 0.2 };
            trainX[11] = new double[] { 0.4, 0.3 };
            trainX[12] = new double[] { 0.5, 0.1 };
            trainX[13] = new double[] { 0.5, 0.2 };
            trainX[14] = new double[] { 0.5, 0.3 };
            trainX[15] = new double[] { 0.6, 0.1 };
            trainX[16] = new double[] { 0.6, 0.2 };
            trainX[17] = new double[] { 0.6, 0.3 };

            trainX[18] = new double[] { 0.1, 0.4 };  // upper left
            trainX[19] = new double[] { 0.1, 0.5 };
            trainX[20] = new double[] { 0.1, 0.6 };
            trainX[21] = new double[] { 0.2, 0.4 };
            trainX[22] = new double[] { 0.2, 0.5 };
            trainX[23] = new double[] { 0.2, 0.6 };
            trainX[24] = new double[] { 0.3, 0.4 };
            trainX[25] = new double[] { 0.3, 0.5 };
            trainX[26] = new double[] { 0.3, 0.6 };

            /// Label Data 
            int[][] trainY = new int[27][];
            trainY[0] = new int[] { 1, 0, 0 };  // class 0
            trainY[1] = new int[] { 1, 0, 0 };
            trainY[2] = new int[] { 1, 0, 0 };
            trainY[3] = new int[] { 1, 0, 0 };
            trainY[4] = new int[] { 1, 0, 0 };
            trainY[5] = new int[] { 1, 0, 0 };
            trainY[6] = new int[] { 1, 0, 0 };
            trainY[7] = new int[] { 1, 0, 0 };
            trainY[8] = new int[] { 1, 0, 0 };

            trainY[9] = new int[] { 0, 1, 0 };  // class 1
            trainY[10] = new int[] { 0, 1, 0 };
            trainY[11] = new int[] { 0, 1, 0 };
            trainY[12] = new int[] { 0, 1, 0 };
            trainY[13] = new int[] { 0, 1, 0 };
            trainY[14] = new int[] { 0, 1, 0 };
            trainY[15] = new int[] { 0, 1, 0 };
            trainY[16] = new int[] { 0, 1, 0 };
            trainY[17] = new int[] { 0, 1, 0 };

            trainY[18] = new int[] { 0, 0, 1 };  // class 2
            trainY[19] = new int[] { 0, 0, 1 };
            trainY[20] = new int[] { 0, 0, 1 };
            trainY[21] = new int[] { 0, 0, 1 };
            trainY[22] = new int[] { 0, 0, 1 };
            trainY[23] = new int[] { 0, 0, 1 };
            trainY[24] = new int[] { 0, 0, 1 };
            trainY[25] = new int[] { 0, 0, 1 };
            trainY[26] = new int[] { 0, 0, 1 };
  // Learning Rate, epoch 

            double lr = 0.01;
            int maxEpoch = 1000;
            Console.WriteLine("\nStart online SGD train lr = " +
              lr.ToString("F3") + " maxEpoch = " + maxEpoch);
            double[][] wts = Train(trainX, trainY, lr, maxEpoch);
            
            Console.WriteLine("Done");

            Console.WriteLine("\nModel weights and biases:");
            ShowMatrix(wts);

            Console.WriteLine("\nPredicting class for [0.45, 0.25] ");
            double[] x = new double[] { 0.45, 0.25 };
            double[] oupts = ComputeOutput(x, wts, true);  // true: show pre-softmax
            ShowVector(oupts);

            Console.WriteLine("\nEnd demo");
            Console.ReadLine();

Hàm Softmax

 static double[] Softmax(double[] vec)
        {
            // naive. consider max trick
            double[] result = new double[vec.Length];
            double sum = 0.0;
            for (int i = 0; i < result.Length; ++i)
            {
                result[i] = Math.Exp(vec[i]);
                sum += result[i];
            }
            for (int i = 0; i < result.Length; ++i)
                result[i] /= sum;
            return result;
        }

Hàm Loss

Gradient Descent